集合运算方法概述
- 集合的概念
集合是由确定的、互不相同的元素组成的一个整体。在数学中，集合运算是对集合元素进行操作的方法。
- 常见的集合运算
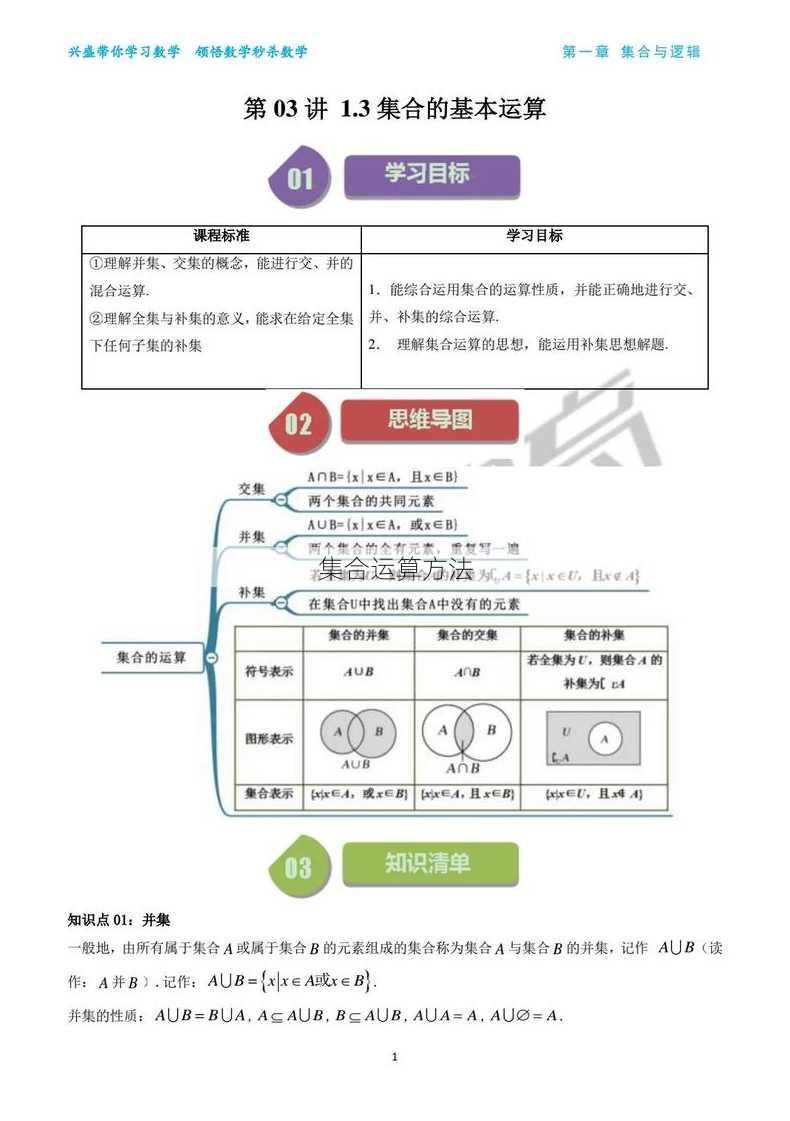
并集（∪）：两个集合A和B的并集是指包含A和B中所有元素的集合。
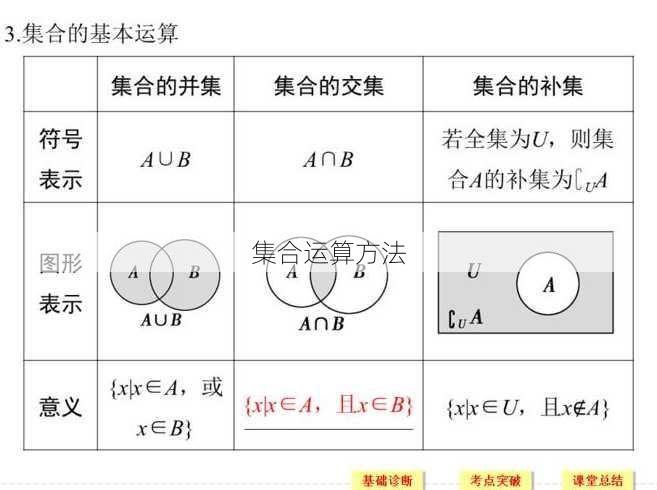
交集（∩）：两个集合A和B的交集是指同时属于A和B的元素组成的集合。
差集（A - B）：集合A减去集合B，即属于A但不属于B的元素组成的集合。
补集：对于全集U和集合A，A的补集是指全集U中不属于A的元素组成的集合。
集合运算的具体方法
- 交集运算
交集运算可以通过以下方法进行：
元素法：直接找出两个集合共有的元素。
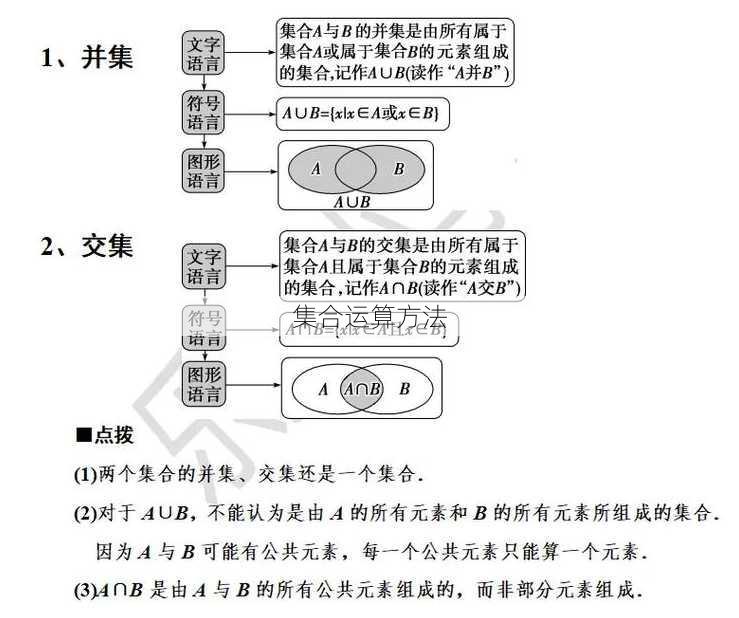
图示法：用Venn图表示两个集合，找出重叠部分。
- 并集运算
并集运算可以通过以下方法进行：
元素法：将两个集合的元素合并，去除重复元素。
图示法：用Venn图表示两个集合，将两个集合合并。
- 差集运算
差集运算可以通过以下方法进行：
元素法：找出属于A但不属于B的元素。
图示法：用Venn图表示两个集合，从集合A中去除与集合B重叠的部分。
集合运算的实际应用
集合运算在数学、计算机科学、统计学等领域都有广泛的应用。例如，在计算机科学中，集合运算可以用于数据库查询、算法设计等。
集合运算的注意事项
元素唯一性：集合中的元素是唯一的，不能重复。
确定性：集合运算的结果必须是确定的，不能有歧义。
FAQs
Q1：什么是集合运算？
A1： 集合运算是对集合元素进行操作的方法，包括并集、交集、差集等。
Q2：如何进行交集运算？
A2： 可以通过元素法或图示法进行交集运算。
Q3：如何进行并集运算？
A3： 可以通过元素法或图示法进行并集运算。
Q4：如何进行差集运算？
A4： 可以通过元素法或图示法进行差集运算。
Q5：集合运算有哪些实际应用？
A5： 集合运算在数学、计算机科学、统计学等领域都有广泛的应用，例如数据库查询、算法设计等。
文章版权声明：除非注明，否则均为清梦网原创文章，转载或复制请以超链接形式并注明出处。